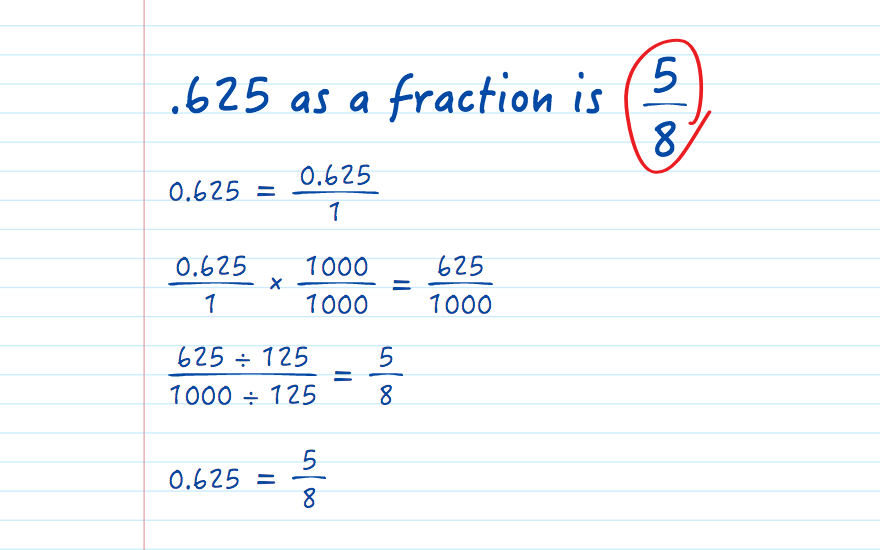When it comes to understanding how decimals relate to fractions, the concept of converting .625 as a fraction becomes an essential topic to explore. Fractions and decimals are closely related, and knowing how to convert between the two can simplify many mathematical problems. In this article, we will delve into the intricacies of converting .625 into a fraction, providing you with a clear and comprehensive understanding of the process.

Fractions are an integral part of mathematics, used in everyday life, from cooking to construction. Converting decimals like .625 into fractions is a fundamental skill that can help you solve various problems efficiently. Whether you're a student, a teacher, or someone who enjoys learning about mathematics, this article will guide you step by step.

This guide will cover everything you need to know about .625 as a fraction, including definitions, methods, and practical examples. By the end of this article, you'll have a thorough understanding of how to convert .625 into a fraction and why it matters in real-world applications.

Read also:
Diva Flawless Unveils New Sex Videos A Deep Dive

What is a Fraction?
Understanding Decimals
Converting Decimal to Fraction
Converting .625 to a Fraction
Simplified Form of .625 as a Fraction
Common Equivalent Fractions
Practical Applications of .625 as a Fraction
Tips for Converting Decimals to Fractions
Common Mistakes to Avoid
Conclusion

What is a Fraction?

A fraction represents a part of a whole. It is written as two numbers separated by a line: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts are being considered, while the denominator shows the total number of equal parts in the whole.

Fractions can represent values less than one, greater than one, or even whole numbers. For example, 1/2, 3/4, and 5/5 are all fractions. Understanding fractions is essential for many mathematical operations and real-life applications.

Types of Fractions

There are three main types of fractions:

Proper Fractions: The numerator is smaller than the denominator (e.g., 3/5).
Improper Fractions: The numerator is larger than or equal to the denominator (e.g., 7/4).
Mixed Numbers: A combination of a whole number and a proper fraction (e.g., 2 1/3).

Understanding Decimals

A decimal is another way of representing numbers that are not whole. It uses a decimal point to separate the whole number from the fractional part. For example, the number 0.625 consists of zero whole units and 625 thousandths.

Decimals are widely used in everyday life, especially in measurements, currency, and scientific calculations. Converting decimals to fractions allows for easier manipulation and comparison of values.

Converting Decimal to Fraction

Converting a decimal to a fraction involves a few simple steps:

Read also:
Did Emma Miskew Have A Baby Unveiling The Truth Behind The Headlines

Write the decimal as a fraction with the decimal number as the numerator and 1 as the denominator.
Multiply both the numerator and denominator by 10 for every digit after the decimal point.
Simplify the resulting fraction, if possible.

This method ensures that the decimal is accurately represented as a fraction.

Why Convert Decimals to Fractions?

Converting decimals to fractions is useful for several reasons:

Fractions are often easier to work with in mathematical operations such as addition, subtraction, multiplication, and division.
Fractions provide a clearer representation of exact values, especially in situations where precision is critical.
Fractions are commonly used in recipes, construction, and other real-world applications.

Converting .625 to a Fraction

Now, let's apply the conversion method to .625:

Write .625 as a fraction: 0.625/1.
Multiply both numerator and denominator by 1000 (since there are three digits after the decimal point): (0.625 × 1000) / (1 × 1000) = 625/1000.
Simplify the fraction: 625/1000 can be reduced to 5/8 by dividing both numerator and denominator by their greatest common divisor (125).

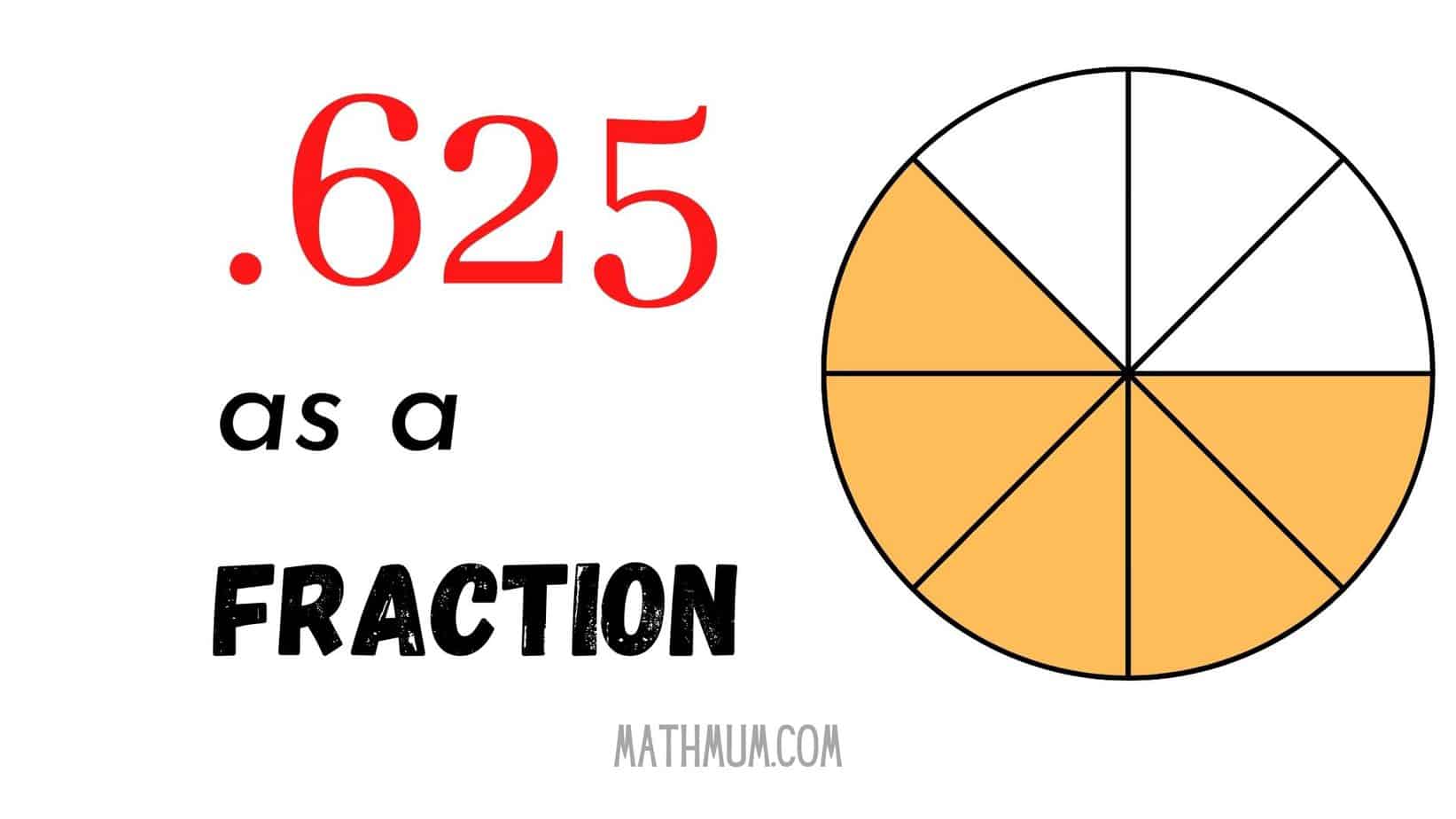
Therefore, .625 as a fraction is 5/8.

Steps to Simplify Fractions

Simplifying fractions involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by this number. For example, in the case of 625/1000:

The GCD of 625 and 1000 is 125.
Divide both numerator and denominator by 125: 625 ÷ 125 = 5, and 1000 ÷ 125 = 8.
The simplified fraction is 5/8.

Simplified Form of .625 as a Fraction

The simplified form of .625 as a fraction is 5/8. This fraction is in its lowest terms, meaning it cannot be reduced further. Understanding this concept is crucial for solving more complex mathematical problems involving fractions.

Using simplified fractions makes calculations easier and more efficient. For example, when adding or subtracting fractions, having them in their simplest form ensures that the denominators align correctly.

Why is Simplification Important?

Simplification is important because:

It reduces the complexity of fractions, making them easier to work with.
It ensures accuracy in calculations, especially when dealing with large numbers.
It provides a standardized representation of fractions, which is essential in many fields, including engineering, finance, and education.

Common Equivalent Fractions

Equivalent fractions are fractions that represent the same value but have different numerators and denominators. For example, 5/8 is equivalent to 10/16, 15/24, and 20/32. These fractions all simplify to 5/8.

Understanding equivalent fractions is useful for comparing values and solving problems that involve fractions with different denominators.

How to Find Equivalent Fractions

To find equivalent fractions:

Multiply both the numerator and denominator by the same number.
For example, to find an equivalent fraction for 5/8, multiply both by 2: (5 × 2) / (8 × 2) = 10/16.

Practical Applications of .625 as a Fraction

Converting .625 to a fraction has several practical applications:

Cooking: Recipes often use fractions to measure ingredients. Knowing that .625 is equivalent to 5/8 can help in adjusting recipes accurately.
Construction: Fractions are used in measurements for building materials. Understanding .625 as a fraction ensures precise cutting and fitting of materials.
Science and Engineering: Fractions are used in calculations involving ratios, proportions, and measurements.

These applications demonstrate the importance of understanding fractions in everyday life and professional fields.

Tips for Converting Decimals to Fractions

Here are some tips to make the conversion process easier:

Always write the decimal as a fraction first, with the decimal number as the numerator and 1 as the denominator.
Multiply both numerator and denominator by 10 for every digit after the decimal point.
Simplify the fraction by finding the greatest common divisor (GCD) and dividing both numerator and denominator by it.

Practicing these steps regularly will improve your ability to convert decimals to fractions quickly and accurately.

Common Mistakes to Avoid

When converting decimals to fractions, some common mistakes include:

Forgetting to multiply both numerator and denominator by the same number.
Failing to simplify the fraction to its lowest terms.
Misplacing the decimal point when writing the fraction.

Avoiding these mistakes will ensure accurate results and improve your overall understanding of fractions.

Conclusion

Converting .625 to a fraction is a straightforward process that involves writing the decimal as a fraction, multiplying by a power of ten, and simplifying the result. The simplified form of .625 as a fraction is 5/8. Understanding this concept is essential for solving mathematical problems and applying fractions in real-world situations.

We encourage you to practice converting decimals to fractions regularly to enhance your skills. If you found this article helpful, please share it with others and explore more content on our website. Leave a comment below if you have any questions or suggestions for future topics.